We use cookies to make your experience better. To comply with the new e-Privacy directive, we need to ask for your consent to set the cookies. Learn more.
Blog - How to Calculate Spring Constant
All technical springs have the property that they undergo an elastic deformation under the influence of a force or moment. The twisted spring constantly wants to return to its original shape. The reshaping of the spring causes the spring to bring back load in Newtons. A number of things with which a designer can influence the spring travel and the damping of a spring element are: Choice of materials, Design (eg compression spring in conical, barrel or hourglass shape), Choice of medium (eg gases or liquids as damping between material).
In this piece we explain:
What is a spring constant?
A spring constant is the force in Newtons that a spring produces under pressure. A spring constant is expressed in Newtons per millimeter of compression, or Newtons per º twisted. The º mainly applies to torsion springs. For springs with higher forces, such as nitrogen gas springs, DecaNewton (daN) is used. One "daN" is equal to 10 Newtons.
Types of forces
There are three types of forces that springs provide (excluding exceptions such as constant force springs). The forces depend on the aforementioned parts of the design and type of spring.
- Linear force springs,
- Progressive force springs,
- Regressive Force Springs.
Linear force springs
With these springs, the load and the suspension travel are in proportion. Provided that the material behaves ideally (by Hooke's law σ=E.ε ). In addition, it is a condition that the spring does not acquire internal friction with an ideal linear force, because this causes heating. In practice, perfectly linear springs do not actually exist, but a lot of pressure, tension and torsion springs come so close that with a relatively small margin of error these springs can speak of a spring constant.
Progressive force springs
The spring becomes stiffer with higher load. We see this in designs where forces are unpredictable, suspension springs are a good example of this. The suspension spring must be able to spring back at a threshold, but also at a hole in the road. If the suspension spring were to provide a linear force here, the car would be damaged. These springs do not provide constant forces, which is why they do not have a spring constant.
Regressive force
The spring becomes more flexible with more force. We mainly see this characteristic in disc springs. Above a ratio of 1.5 (Height : Thickness Steel) the disc spring shows more and more regressive characteristics and is able to push through therefore the spring must be fully supported. At ratios greater than 2, the disc springs may reverse when brought to the flat position. These springs do not provide constant forces, which is why they do not have a spring constant.

How do you calculate a spring rate?
The loads on a technical spring are indicated by a force F (Newton) which results in a spring travel s (mm) or a load T (º) (=F*r) which results in an angular deflection φ (torsion springs). The relationship between the load and the resulting displacement can be plotted in a graph (spring diagram). The line indicating this relationship is called the spring characteristic. The tangent of the inclination angle α of the spring characteristic is called the spring constant R (C/nmm).
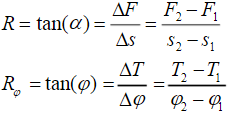
The tan(α) calculation is the calculation for the spring stiffness of the compression and extension springs, the tan (φ) calculation is for torsion springs.